RSA 生成、加密、解密、原理介绍。
RSA 算法是一种非对称加密算法,由 Ron Rivest、Adi Shamir 和 Leonard Adleman 在 1977 年提出。它广泛应用于数据加密和数字签名。RSA 的安全性基于大整数分解的困难性。下面介绍 RSA 的生成、加密、解密过程及原理。
RSA 实现过程
Setup
选择两个大质数 $p$,$q$
计算 $n=p\times q$
计算 $\varphi(n)=(p-1)(q-1)$
选择公钥指数 $e$,满足 $1<e<\varphi(n)$,$(e,\varphi(n))=1$
通常选择 $e=65537$ (常见公钥指数)
计算私钥指数 $d\equiv e^{-1}\ (mod\ \varphi(n))$
如此,生成了公钥 $(e,n)$,私钥 $(d,n)$
Encrypt
将明文 $M$ 转换为一个整数 $m$,$0\le m<n$
计算密文 $C=m^e\ (mod\ n)$
Decrypt
- 计算 $m=C^d(mod\ n)$
- 将整数 $m$ 转换回明文 $M$
原理
解密如何恢复明文 $M$
$$
C^d\equiv (m^e)^d\equiv m^{e\times d}\ (mod\ n)
$$
根据
$$
e\times d\equiv 1(mod\ \varphi(n))\to e\times d=k\varphi(n)+1\ (k\in Z)
$$
因此,根据扩展欧拉定理,由于 $n$ 的质因子最大次数为 $1$,有
$$
m^{e\times d}= m^{k\varphi(n)+1}\equiv m\ (mod\ n)
$$
实现一个 RSA 加密
首先选定大质数,这里选了一个
450 位的 $p$ :
467032132547092763679424400715256463886919640292692842040806542563367226725988741211988934394123174820184618017031738160277150838885208581046672621508843714520278468042250870431095176254092110937655506062205085436582547423982296948571938215345771568040915899620766342701069979208453111021040357978976240267500147399135034516743657768591495774709227690312443802901609681833792358656331078133513494970768837172360779848429580950889376484034920940658301
360 位的 $q$ :
194023861529273746032867033852522503340514249488152902490464389801793788010752676566875987256843797696782133675078829671941265886507529918064352176666215307571570050799028252465780168559345383973414460523204995557736345483058886026979041604309477595545435812870900720402574135711051824454515829105419317883351244121334629093500195092694732201088610121696992369
按上述实现流程完成代码。(由于涉及到超大整数,使用 python 完成)
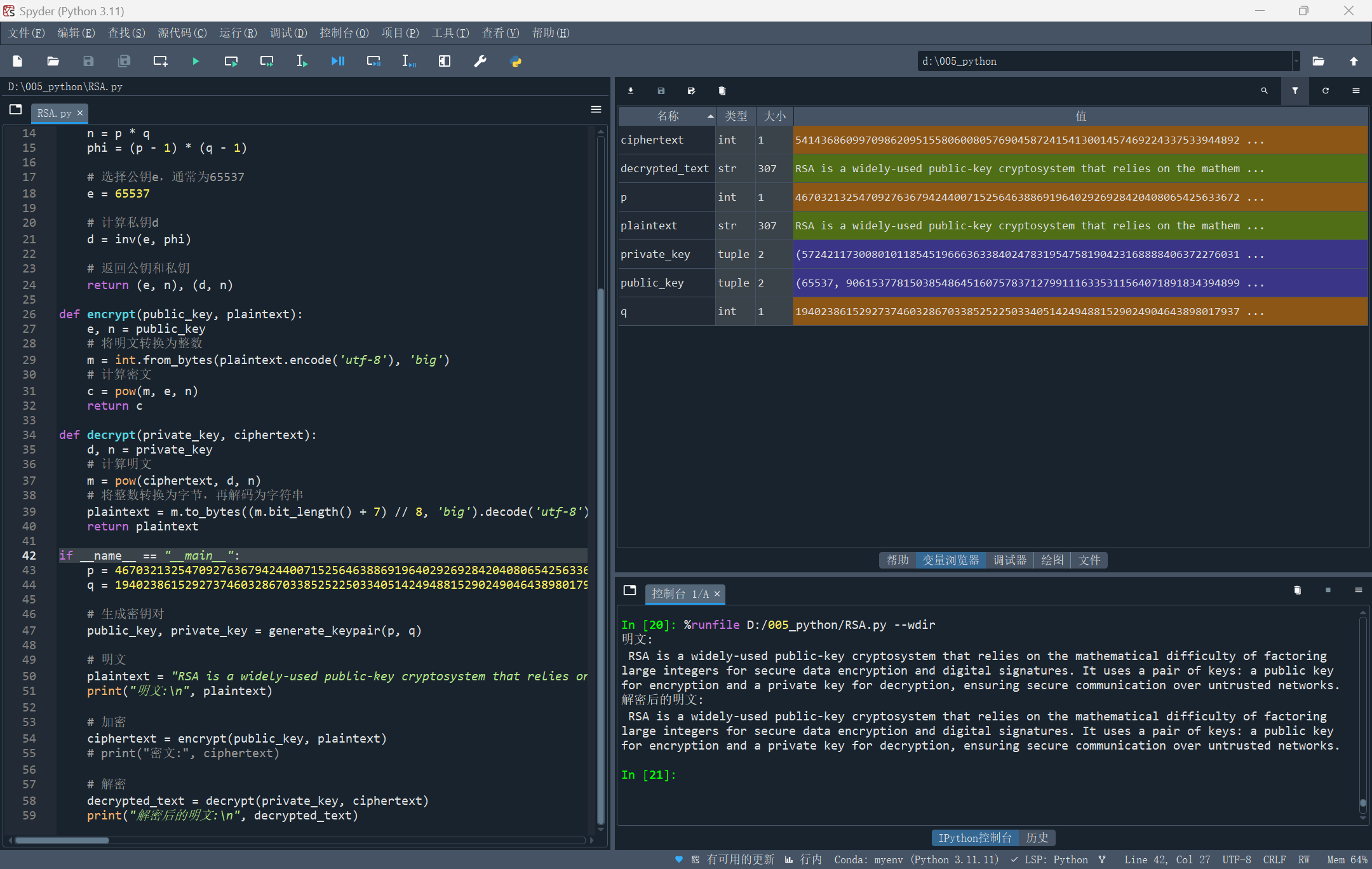
这样,我们就实现了一个非对称加密算法。
1 | def exgcd(a, b): |