三阶魔方,一个43252003274489856000阶的群。
前言
对群的性质熟悉的同学在看到这个title后只需短暂思考几秒,就不难发现,把对魔方的每一个操作看作一个元素,魔方简直就是一个非常标准的群:
1.可结合:$(RU)R$ 和 $R(UR)$ 完全一致。
2.有单位元:不进行任何操作就是单位元。
3.有逆元:$R$ 逆元 $R’$,$RUL$ 逆元 $L’U’R’$,任何操作的逆操作就是它的逆元。
写到这里给对魔方不熟悉的小伙伴放一张图解释一下:
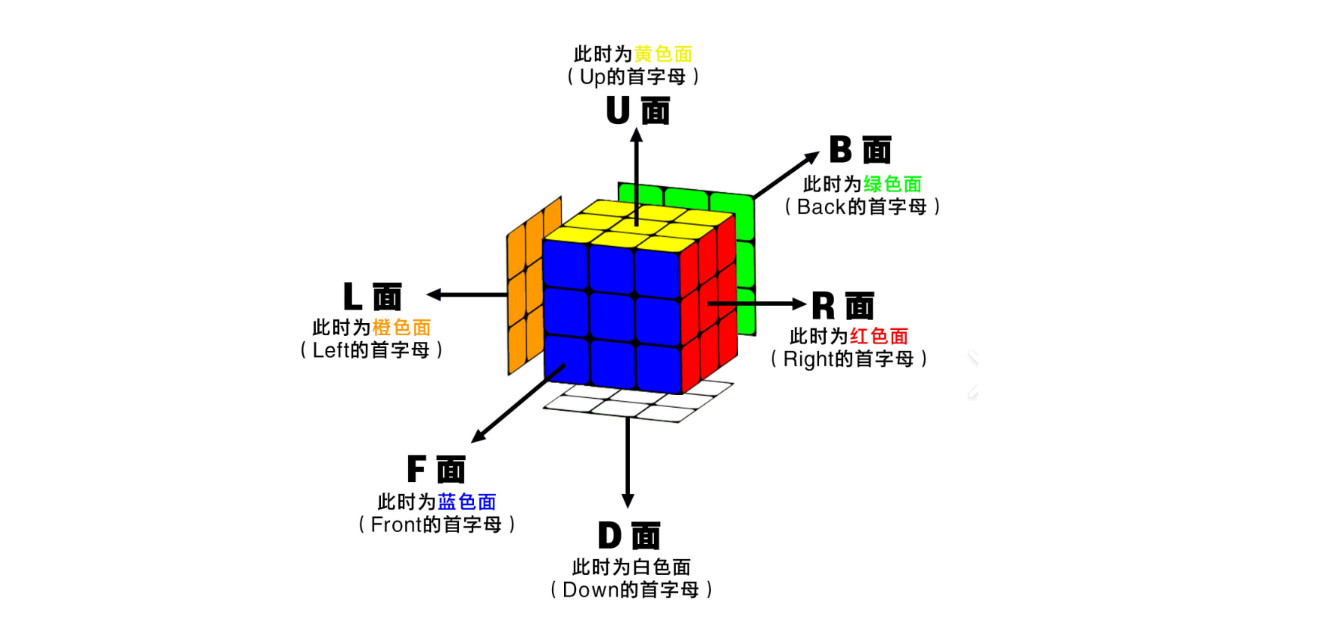
U对应的操作就是将U面顺时针转动90°U'对应的操作就是将U面逆时针转动90°R对应的操作就是将R面顺时针转动90°
……
相信你已经对“魔方”是一个“群”这个观点初步认可了,下面开始探究:这个“群”有什么性质,这个视角能为我们带来什么…
魔方群的元素
首先,我们可以给出这个三阶魔方群中的一些最基本的元素:不操作(单位元),$R$ ,$R’$ ,$U$ ,$U’$ ,$L$ ,$L’$ ,$B$ ,$B’$ ,$D$ ,$D’$ ,$F$ ,$F’$ 。
其他所有的元素都可以由这些基本元素组合而成。
我们记集合 G 为上述所有基本元素任意组合而成的元素。 不难发现,以 G 为集合的代数系统是不构成群的:元素的逆元不唯一了。如:单位元的逆元,既可以是单位元,也可以是 $RR’$,$U’U$ 等等,即魔方中不同的操作可以达成相同的效果。
因此,希望魔方真正意义上成为一个群,我们需要做一些修正:在集合 G 上规定一个等价关系 R,当两个操作a, b的运算结果相同时,认为 aRb,即a操作与b操作等价。
有了这个等价关系,取 S 为 G 关于 R 的等价类的集合,记作 S = G / R 。在 S 集合下,每一个元素(等价类)都有唯一对应的逆元(等价类),”魔方”正式成为了一个”群”。
魔方群的阶
你是否跟我一样好奇,一个魔方有多少种打乱状态呢。计算是这样的:
$$
\frac{8!\times3^8\times12!\times2^{12}}{3\times2\times2}=43252003274489856000
$$
有超过4.3千亿亿种打乱状态。(顺带提一句,目前通过计算机验证,任何一种打乱状态都可以在20步以内还原,很神奇吧)
接下来说说这个计算是怎么来的。
六个中心块固定朝向后,就不能翻转魔方了,此时:
8个角块有 8! 种摆放方式;
每个角块3个朝向,故角块共有 $3^8$ 种朝向情况;
12个棱块有 12! 种摆放方式;
每个棱块2个朝向,故棱块共有 $2^{12}$ 种朝向情况;
保持其他色块不动,不可单独改变一个角块朝向,不可单独改变一个棱块朝向,不可单独交换一对棱块或一对角块的位置,故总情况数需分别除以3,2,2。
至此,我们知道,三阶魔方是一个43252003274489856000阶的有限群。
既然是有限群,就应该具有有限群的性质了:对任意元素 $a$,都存在一个周期 $r$,使得 $a^r=e$ 。
对应到魔方上就是:对一个还原的魔方循环重复任何一个操作,总会重新回到还原状态。
little tip
Q:学会从群论的视角看魔方能让我从sub20进步到sub10吗?
A:不能。