小花生

study & life record.

第十二届蓝桥杯软件赛省赛C++ A组

发表于 分类于 ，

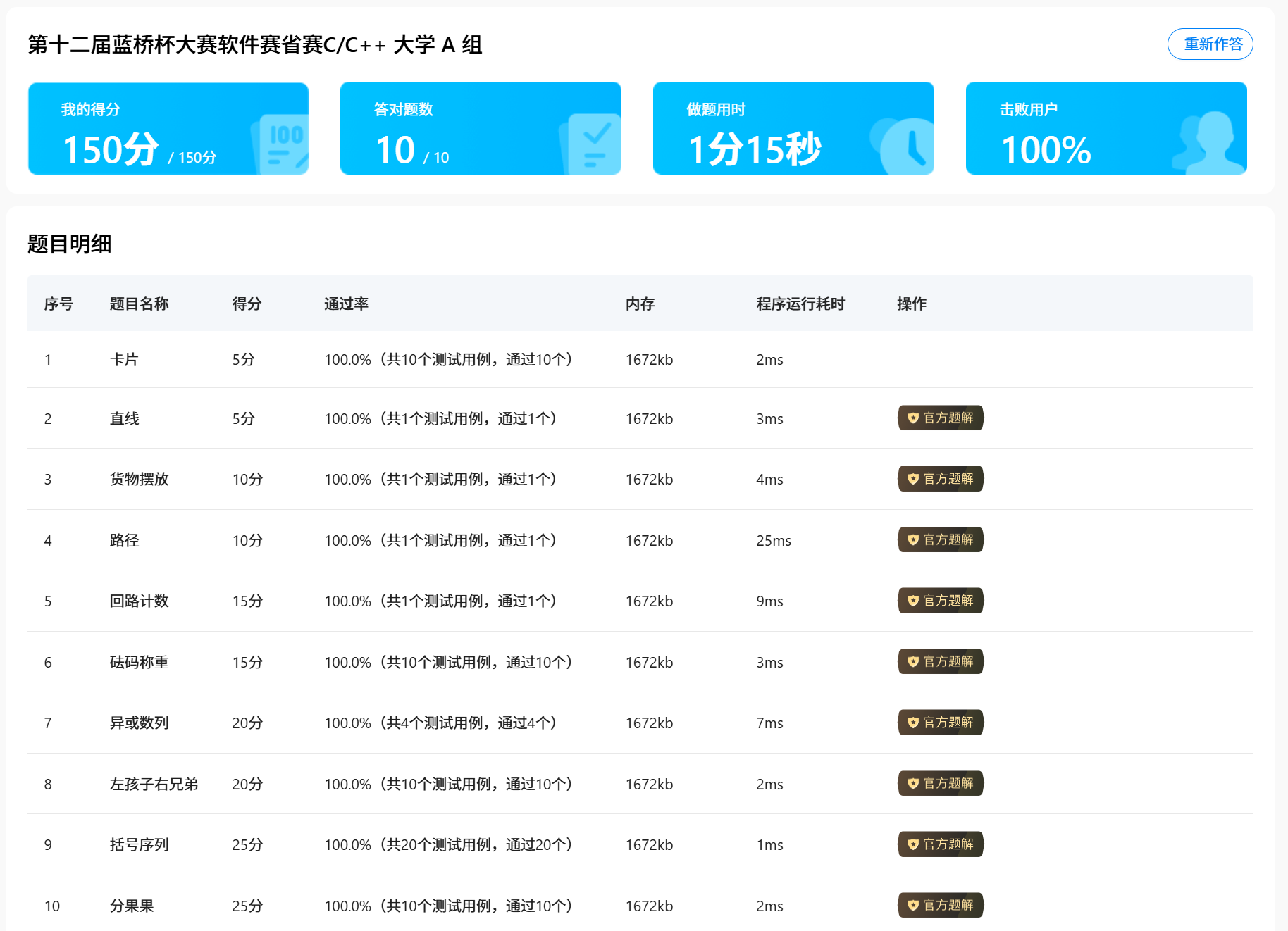
第十二届蓝桥杯软件赛省赛C++ A组 题解。

以下代码均通过测试，可放心食用。

本期知识点：最短路，状压 dp，博弈，DFS，多维 dp。

填空题

2. 直线

数据不大，直接暴力所有选点，将可能的直线加入 set 中，最后返回 set 的大小即可。注意这里处理斜率不存在的直线，不加入 set，最后计数时再直接加上。输出 40257。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#include<bits/stdc++.h>
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef pair<double, double> PDD;

void solve(){
    int n, m; cin >> n >> m;    
    
    vector<PII>p(n * m);
    set<PDD>st;

    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            p[i * m + j] = {i, j};
        }
    }

    for(int i = 0; i < p.size(); i++){
        for(int j = i + 1; j < p.size(); j++){
            auto [x1, y1] = p[i];
            auto [x2, y2] = p[j];
            if(x1 == x2) continue;
            double k = 1.0 * (y2 - y1) / (x2 - x1);
            double b = 1.0 * (x2 * y1 - x1 * y2) / (x2 - x1);
            st.emplace(k, b);
        }
    }

    cout << st.size() + n;
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
    return 0;
}

3. 货物摆放

题意：将 n 拆成 3 个数的乘积，求有多少种拆法。

做质因数分解：$n=p_1^{q_1}p_2^{q_2}\cdots p_k^{q_k}$，分别处理不同质因子，乘法原理即可。

对于一个 $p_i^{q_i}$，希望将 $q_i$ 拆分为 3 个自然数(0, 1, …) 的和，这就是高中常处理的隔板问题，方案数 $C_{q_i+2}^2$。

因此最终结果应为 $\prod\limits_{i=1}^k C_{q_i+2}^2$，输出结果 2430。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
#define int long long
using namespace std;

void solve(){
    int n; cin >> n;
    
    vector<int>p;
    for(int i = 2; i * i <= n; i++){
        if(n % i == 0){
            int u = 0;
            while(n % i == 0){
                u++; n /= i;
            }
            p.emplace_back(u);
        }
    }
    if(n != 1) p.emplace_back(1);
    
    int res = 1;
    for(auto &i : p){
        res *= (i + 2) * (i + 1) / 2;
    }
    cout << res;
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
    return 0;
}

4. 路径

直接按题意建图，跑一遍最短路即可，输出 10266837。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<bits/stdc++.h>
#define int long long
using namespace std;
typedef pair<int, int> PII;


void solve(){
    int n; cin >> n;
    vector<vector<PII>>adj(n + 1);

    for(int i = 1; i <= n; i++){
        for(int j = i + 1; j <= i + 21 && j <= n; j++){
            int w = lcm(i, j);
            adj[i].emplace_back(w, j);
            adj[j].emplace_back(w, i);
        }
    }

    vector<int>dist(n + 1, 1e9); dist[1] = 0;
    vector<bool>vis(n + 1, 0);
    priority_queue<PII, vector<PII>, greater<PII>>Q;
    Q.emplace(0, 1);
    while(!Q.empty()){
        int u = Q.top().second; Q.pop();

        if(vis[u]) continue;
        vis[u] = 1;

        for(auto &[d, v] : adj[u]){
            if(dist[v] > dist[u] + d){
                dist[v] = dist[u] + d;
                Q.emplace(dist[v], v);
            }
        }
    }
    cout << dist[n];
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
    return 0;
}

5. 回路计数

题意：求图中经过所有点的哈密尔顿回路个数。

第一想法是，数据 $n=21$ 不大，试试 dfs 能不能过，写完跑不出结果，一算 $n!$ 近似 $5e19$，显然跑不下来。

正解是状压 dp，在（已经经过哪些点）的集合之间转移。

dp[i][j] 表示，节点集合 i 中, 以 j 为结尾的路径的数量，直接在不同集合间转移即可，最后汇总满集合的路径总数量。时间复杂度 $O(n^22^n)$ ，最大近似 $9e8$，能跑下来，最终输出 881012367360。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<bits/stdc++.h>
#define int long long
using namespace std;

void solve(){
    int n; cin >> n;
    
    vector<vector<bool>>g(n, vector<bool>(n));
    vector<vector<int>>dp(1 << n, vector<int>(n));
    // dp[i][j] 表示, 节点集合 i 中, 以 j 为结尾的路径的数量

    for(int i = 1; i <= n; i++){
        for(int j = i + 1; j <= n; j++){
            if(gcd(i, j) == 1){
                g[i - 1][j - 1] = g[j - 1][i - 1] = 1;
            }
        }
    }

    dp[1][0] = 1;
    for(int i = 0; i <= 1 << n; i++){
        for(int j = 0; j < n; j++){
            if(i >> j & 1){
                for(int k = 0; k < n; k++){
                    if(i - (1 << j) >> k & 1 && g[k][j]){
                        dp[i][j] += dp[i - (1 << j)][k];
                    }
                }
            }
        }
    }

    int res = 0;
    for(int i = 1; i < n; i++) res += dp[(1 << n) - 1][i];
    cout << res;
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
    return 0;
}

程序题

1. 卡片

不难发现，$\dfrac{k(k+1)}{2}\ge n$，已知 $n$ 倒推最小的 $k$ 即可。

$n$ 范围 $1e9$，很多方法都可以，遍历 $O(\sqrt n)$，二分 $O(\log n)$，求根式解 $O(1)$，挑一个写就好了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<bits/stdc++.h>
#define int long long
using namespace std;

void solve(){
    int n; cin >> n;
    
    int l = 0, r = 1e5;
    while(l + 1 != r){
        int mid = l + r >> 1;
        if(mid * (mid + 1) >= 2 * n) r = mid;
        else l = mid;
    }

    cout << r;
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
    return 0;
}

6. 砝码称重

没什么好说的，直接模拟就可以了，每多一个砝码，在原有可称重量上转移。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<bits/stdc++.h>
#define int long long
using namespace std;

void solve(){
    int n; cin >> n;
    vector<int>a(n);
    for(int i = 0; i < n; i++) cin >> a[i];

    set<int>st;
    st.emplace(0);

    for(auto &i : a){
        auto tmp = st;
        for(auto &u : tmp){
            st.emplace(u + i);
            if(u - i > 0) st.emplace(u - i);
            if(i - u > 0) st.emplace(i - u);
        }
    }
    cout << st.size() - 1;
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
    return 0;
}

7. 异或数列

比较两数大小即比较谁有更高位的 1，从高位往低位比较：

  • 如果该位的 1 个数为偶数，那么无论两人怎么取，在该位上两人都会相同，因此此位无影响，继续比较下一位。
  • 如果该位的 1 个数为奇数，不难发现，掌控着最后一个 1 的人取得胜利。
    • 如果只有一个 1，那么 Alice 拿去，Alice 胜。
    • 如果此位 0 的个数为偶数，那么 Alice 先拿 1，场上剩下的 0 和 1 都为偶数，接下来只需要 Bob 拿什么，Alice 拿什么，就一定能拿到最后一个 1，Alice 胜。
    • 如果此位 0 的个数为奇数，那么第一次取数时，无论 Alice 拿什么，Bob 拿相反的，场上剩下的 0 和 1 都为偶数，接下来只需要 Alice 拿什么，Bob 拿什么，就一定能拿到最后一个 1，Bob 胜。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<bits/stdc++.h>
#define int long long
using namespace std;

void solve(){
    int n; cin >> n;
    vector<int>a(n);
    for(int i = 0; i < n; i++) cin >> a[i];

    vector<int>p(21);
    for(int k = 0; k < 21; k++){
        for(int i = 0; i < n; i++){			
            p[k] += (a[i] >> k) & 1;
        }
    }

    for(int i = 20; i >= 0; i--){
        if(p[i] % 2 == 0) continue;
        if(p[i] == 1){
            cout << 1 << '\n';
            return;
        }
        if(n % 2 == 1){
            cout << 1 << '\n';
            return;
        }
        cout << -1 << '\n';
        return;
    }
    cout << 0 << '\n';
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    int t; cin >> t;
    while(t--) solve();
    return 0;
}

8. 左孩子右兄弟

难点大概在从题目简短的描述中读懂左孩子右兄弟的转换方法……

不难发现，当前子树的最大深度，为自身的孩子个数，加上某个孩子为根的子树的最大深度，如此 dfs 即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
#define int long long
using namespace std;

void solve(){
    int n; cin >> n;
    vector<vector<int>>adj(n + 1);
    for(int i = 2; i <= n; i++){
        int p; cin >> p;
        adj[p].emplace_back(i);
    }

    function<int(int)>dfs = [&](int u){
        int res = 0;
        for(auto &v : adj[u]){
            res = max(res, dfs(v));
        }
        return res + adj[u].size();
    };
    cout << dfs(1);
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
    return 0;
}

9. 括号序列

  • Hint 1：加入 ( 、) 互不影响。

不难发现，存在一个分割位置，在分割位置前，只加入 (，在分割位置后，只加入 )。计算总方案时，只需利用乘法原理将两种添加括号的方案数相乘即可，下面只考虑加入左括号。

  • Hint 2：加入 ( 的不同位置有多少种？

实际上，由于以 ) 做分割，每一个 ) 前的位置都可以添加 (。因此能够添加 ( 的位置个数即为 ) 的个数。

  • Hint 3：一共要加入多少个 ( ？

未匹配的 ) 有多少个，就加多少个。

  • Hint 4：不同加入 ( 的位置的限制是？

当前位必须满足紧跟其后 ) 已完成匹配。

解：用 min_p 记录当前 ) 所需的最小 ( 数，dp[i][j] 表示考虑第 i 个 )，已经使用 j 个 ( 的方案数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include<bits/stdc++.h>
#define int long long
using namespace std;

constexpr int mod = 1e9 + 7;

void solve(){
    string s; cin >> s;

    auto cal = [](string s) -> int{
        int t = 0, all = 0, p = 0;
        // t 记录满足匹配条件, all 记录 ')' 个数, p 记录需要的 '(' 个数 
        vector<int>min_p(1);
        for(auto &u : s){
            if(u == '(') t++;
            else{
                all++;
                if(--t < 0){
                    t = 0;
                    p++;
                }
                min_p.emplace_back(p);
            }
        }

        vector<vector<int>>dp(all + 1, vector<int>(p + 1));
        vector<vector<int>>pre(all + 1, vector<int>(p + 1));

        dp[0][0] = 1;
        for(int j = 0; j <= p; j++) pre[0][j] = 1;

        for(int i = 1; i <= all; i++){
            for(int j = min_p[i]; j <= p; j++){
                dp[i][j] = pre[i - 1][j];
            }
            pre[i][min_p[i]] = dp[i][min_p[i]];
            for(int j = min_p[i] + 1; j <= p; j++){
                pre[i][j] = pre[i][j - 1] + dp[i][j];
                pre[i][j] %= mod;
            }
        }

        return dp[all][p];
    };
    
    int resl = cal(s);
    reverse(s.begin(), s.end());
    for(auto &u : s) u = '(' + ')' - u;
    int resr = cal(s);
    cout << resl * resr % mod;
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
    return 0;
}

10. 分果果

动态规划，解析见代码。时间复杂度 $O(wn^3)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include<bits/stdc++.h>
#define int long long
using namespace std;

constexpr int inf = 1e9;

void solve(){
    int n, m; cin >> n >> m;
    vector<int>w(n + 1);
    // 直接存储前缀和
    for(int i = 1; i <= n; i++) {
        cin >> w[i];
        w[i] += w[i - 1];
    }

    int res = inf;

    // 枚举最小重量, 复杂度 nw/m
    for(int minn = 1; minn <= w[n] * 2 / m; minn++){
        vector<vector<vector<int>>>dp(m + 1, vector<vector<int>>(n + 1, vector<int>(n + 1, inf)));
        // dp[i][j][k] 表示前 i 个小朋友, 最后一个小朋友分到的糖果区间结束于第 j 包,
        // 且最后一个被重复购买的糖果是第 k 包时的最大重量。
        dp[0][0][0] = minn;
        // 枚举小朋友, 复杂度 m
        for(int i = 1; i <= m; i++){
            // 枚举重复购买的糖果位置, 复杂度 n
            for(int k = 0; k <= n; k++){
                // 指针区间左端点
                int p = 0;
                // 枚举最后一个小朋友糖果区间结束的位置, 复杂度 n
                for(int j = k; j <= n; j++){
                    // 不重复购买糖果
                    if(k > 0){
                        dp[i][j][k] = min(dp[i][j][k], dp[i][j][k - 1]);
                    }
                    // 跟进指针 p
                    while(p < j && w[j] - w[p] >= minn){
                        p++;
                    }
                    // 重复购买
                    if(p > 0){
                        int pp = min(p - 1, k);
                        dp[i][j][k] = min(dp[i][j][k], max(dp[i - 1][k][pp], w[j] - w[pp]));
                    }
                }
            }
            res = min(res, dp[m][n][n] - minn);
        }
    }
    cout << res;
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
    return 0;
}