小花生

study & life record.

第 37 次 CCF_CSP 认证

发表于 分类于 ，

2025年3月CSP，回顾 + 题解。

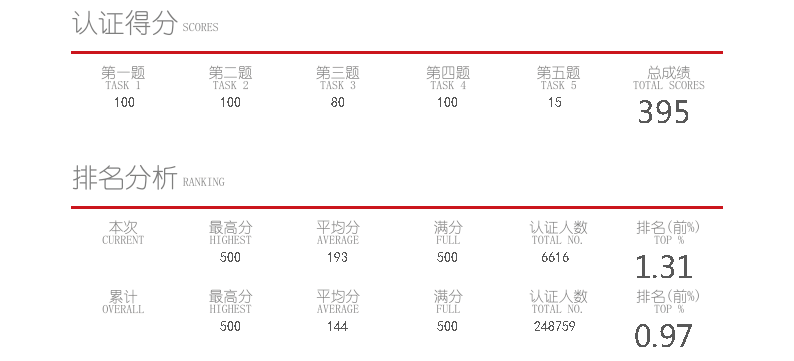
回顾

得分 100 - 100 - 80 - 100 - 15。

T1 T2大概花了 15min，T4 大概 30min 过掉，剩下时间都在写 T3, T5。

本场败笔在 T3，在 DAG 上 DFS 暴搜，没写记忆化，只拿了 80 分。卡在 395，与 400 失之交臂了（哭

T5 Link Cut Tree，神秘的高级数据结构，暂时不补。

题解

数值积分

按题意模拟。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<bits/stdc++.h>
#define int long long
using namespace std;

void solve(){
    int b, c, l, r;
    cin >> b >> c >> l >> r;
    if(l & 1) l++;
    if(r & 1) r--;
    
    int res = 0;
    for(int i = l; i <= r; i += 2){
        res += 2 * (i * i + b * i + c); 
    } 
    cout << res << '\n';
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
    return 0;
}

机器人饲养指南

$$
\sum i = n\ \ \Rightarrow\ \ \max(\sum a_i)
$$

记 $dp[i]$ 为投喂 $i$ 个时的最大快乐值，转移为：
$$
dp[i]=\max_{i-m\le j<i}(dp[j]+a[i-j])
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<bits/stdc++.h>
#define int long long
using namespace std;

void solve(){
    int n, m; cin >> n >> m;
    vector<int> a(m + 1);
    for(int i = 1; i <= m; i++) cin >> a[i];
    
    vector<int> dp(n + 1);
    for(int i = 1; i <= n; i++){
        for(int j = max(0ll, i - m); j < i; j++){
            dp[i] = max(dp[i], dp[j] + a[i - j]);
        }
    }
    cout << dp[n] << '\n';
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
    return 0;
}

模板展开

理解题意：

  • 直接赋值：有点权，无出边

  • 间接赋值：有点权与若干出边，值为自身点权与出边对应点权之和。

那么抽象出来就是一张 DAG，每次修改点权或点权与出边，求值。

对每次 query，做一个记忆化，避免重复搜索。

同时学习一下 istringstream 字符串输入。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include<bits/stdc++.h>
using namespace std;

constexpr int mod = 1e9 + 7;

unordered_map<string, int> StoI;
vector<int> val(1005);
vector<vector<int>> adj(1005);
unordered_map<int, int> mp;

int idx = 1;
inline int get_idx(string s){
    if(StoI[s]) return StoI[s];
    return StoI[s] = idx++;
}

inline int getlen(int x){
    if(mp[x]) return mp[x];
    int res = val[x];
    for(auto &i : adj[x]){
        res += getlen(i);
        res %= mod;
    }
    return mp[x] = res % mod;
}

void solve(){
    int q; cin >> q;
    cin.ignore();

    while(q--){
        string line;
        getline(cin, line);
        istringstream iss(line);

        string op; iss >> op;
        string tmpvar; iss >> tmpvar;
        vector<string> expr; string ex;
        while(iss >> ex) expr.emplace_back(ex);
        // read -> op, var, expr
        int var = get_idx(tmpvar);

        if(op == "1"){
            int sum = 0;
            for(auto &s : expr){
                if(s[0] != '$'){
                    sum += s.size();
                    sum %= mod;
                }
                else{
                    int ss = get_idx(s.substr(1, s.size() - 1));
                    sum += getlen(ss);
                    sum %= mod;
                }
            }
            val[var] = sum;
            adj[var].clear();
        }
        else if(op == "2"){
            adj[var].clear();
            int sum = 0;
            for(auto &s : expr){
                if(s[0] != '$'){
                    sum += s.size();
                    sum %= mod;
                }
                else{
                    int ss = get_idx(s.substr(1, s.size() - 1));
                    adj[var].emplace_back(ss);
                }
            }
            val[var] = sum;
        }
        else{
            cout << getlen(var) << '\n';
        }

        mp.clear();
    }
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
    return 0;
}

集体锻炼

观察到，固定右端点 $r$ 时，区间 $[l, r]$ 的 gcd 可能取值数不超过 $log(r-l+1)$。

因此维护每一段 gcd 不同的区间，每加入一个右端点，更新一遍区间，合并相同区间，逐个区间地去计算贡献。

时间复杂度 $O(n\log n)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<bits/stdc++.h>
#define int long long
using namespace std;

constexpr int mod = 998244353;

int gcd(int a, int b){
    return b ? gcd(b, a % b) : a;
}

struct split{
    int r, g;
    split(int r, int g) : r(r), g(g) {}
};

void solve(){
    int n; cin >> n;
    vector<int>a(n + 1);
    for(int i = 1; i <= n; i++) cin >> a[i];
    
    vector<split>S;
    
    int res = 0;
    
    for(int i = 1; i <= n; i++){
        vector<split>tmp;
        S.emplace_back(i, a[i]);
        for(int j = 0; j < S.size(); j++){
            S[j].g = gcd(S[j].g, a[i]);
            if(tmp.empty()){
                tmp.push_back(S[j]);
            }
            else if(S[j].g == tmp.back().g){
                tmp.back().r = S[j].r;
            }
            else{
                tmp.push_back(S[j]);
            }
        }
        
        S.swap(tmp);

        int sum = S[0].r * (S[0].r + 1) / 2 * S[0].g % mod;
        for(int i = 1; i < S.size(); i++){
            sum += (S[i].r * (S[i].r + 1) / 2 - S[i - 1].r * (S[i - 1].r + 1) / 2) % mod 
                    * S[i].g % mod;
            sum %= mod;
        }
        res += sum * i;
        res %= mod;
    }
    
    cout << res << '\n';
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
    return 0;
}

成绩