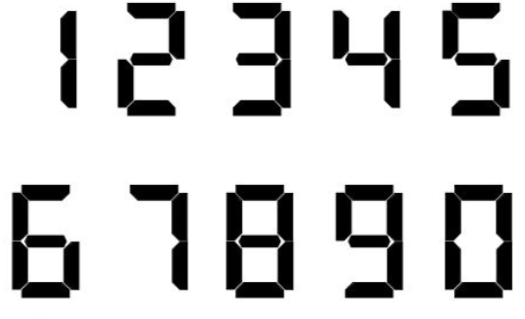牛客周赛 Round 47

牛客周赛 Round 47 补题。

题解

C. 苗苗的气球

分析：对1，2特判，再判断是否有独大的数，如果有，答案是1；如果没有，再讨论 n 的奇偶性，如果是偶数，需要额外删去 1 的个数，因为无法剩下一个奇数。

完整代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    
    int n, sum = 0, cnt1 = 0; cin >> n;
    vector<int>v(n);
    for(auto &i : v){
        cin >> i;
        sum += i;
        if(i == 1) cnt1++;
    }
    int mx = *max_element(v.begin(), v.end());
    
    int ans = 0;
    if(n == 1){
        ans = 1;
    }else if(n == 2){
        ans = v[0] == v[1] ? 0 : 1;
    }else{
        if(mx * 2 >= sum){
            ans = 1;
        }else{
            if(sum % 2 == 0){
                ans = n - cnt1;
            }else{
                ans = n;
            }
        }
    }
    
    cout << ans;
    return 0;
}

D. 萌萌的好数

分析：这种数的规律在每30会复现一次，打表即可。

完整代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;

int a[18] = {1, 2, 4, 5, 7, 8, 10, 11, 14, 16,
            17, 19, 20, 22, 25, 26, 28, 29 };

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    
    int t; cin >> t;
    while(t--){
        int n; cin >> n;
        int u = n / 18, v = n % 18;
        if(v == 0){
            u --, v = 18;
        } v--;
        cout << u * 30 + a[v] << '\n';    
    }
    
    return 0;
}

E. 茜茜的计算器

知识点：快速幂，容斥原理。

分析：分别考虑左右对称和上下对称的数量，再减去重复的数量。

上下对称：1 3 8 0
每个位置都有四种选择，这种情况有 $\displaystyle 4^n$ 种。

左右对称：0-0 8-8 2-5 5-2
这种情况的数量可以只考虑一侧，另一侧自动补齐：
如果是偶数个，有 $\displaystyle 4^{\frac n2}$ 种情况，如果是奇数个，则中间只能放 0, 8，有 $\displaystyle2\times 4^{\frac{n-1}{2}}$ 种情况。
因此无论奇偶，情况数为 $\displaystyle 2^n$ 种。

同时上下对称与左右对称的：
即只以0，8作为左右对称的元素，如果是偶数有 $\displaystyle 2^{\frac n2}$ 种，如果是奇数，有 $\displaystyle 2\times2^{\frac n2}$ 种。
干脆统一为 $\displaystyle 2^{\frac {n+1}2}$ 种。

完整代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;

int qmi(int a, int k, int p){
    int res = 1;
    while(k){
        if(k & 1) res = res * a % p;
        k >>= 1;
        a = a * a % p;
    }
    return res;
}

signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    
    int n, p = 1e9 + 7; cin >> n;
    cout << (qmi(4, n, p) + qmi(2, n, p) - qmi(2, (n + 1) / 2, p) + p) % p;
    
    return 0;
}

F. 花花的地图

分析：通过将消除列的操作转化为加点处理，转换为最短路问题。

完整代码：

#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;

const int N = 2e4, INF = 0x3f3f3f3f;
vector<PII> g[N]; int n, m; 
int dx[4] = {0, -1, 0, 1};
int dy[4] = {1, 0, -1, 0};

int dijkstra(int s){
    priority_queue<PII, vector<PII>, greater<PII>>q;
    vector<int>dist(N, INF);    
    vector<bool>vis(N);    
    dist[s] = 0;
    
    q.emplace(0, s);
    while(!q.empty()){
        int u = q.top().second;
        q.pop();
        
        if(vis[u]) continue;
        vis[u] = 1;
        
        for(auto [w, v] : g[u]){
            if(dist[v] > dist[u] + w){
                dist[v] = dist[u] + w;
                q.emplace(dist[v], v);
            }
        }
    }
    if(dist[n * m - 1] == INF) return -1;
    return dist[n * m - 1];
}

int main(){
    ios::sync_with_stdio(0);
    cin.tie(0);
    
    cin >> n >> m;
    vector<vector<char>> mp(n, vector<char>(m));
    for(int i = 0; i < n; i++)
        for(int j = 0; j < m; j++)
            cin >> mp[i][j];
    vector<int>c(m);
    for(auto &i : c) cin >> i;
    
    for(int i = 0; i < n; i++){
        for(int j = 0; j < m; j++){
            for(int k = 0; k < 4; k++){
                int ii = i + dx[k], jj = j + dy[k];
                if(ii == -1 || ii == n) continue;
                if(jj == -1 || jj == n) continue;
                if(mp[ii][jj] != '#')
                    g[i * m + j].emplace_back(0, ii * m + jj);
                if(j != m - 1)
                    g[i * m + j].emplace_back(c[j + 1], n * m + j + 1);
            }
        }
    }
    
    for(int j = 0; j < m; j++){
        for(int i = 0; i < n; i++){
            g[n * m + j].emplace_back(0, i * m + j);
        }
    }
    
    g[n * m + m].emplace_back(0, 0);
    g[n * m + m].emplace_back(c[0], n * m);
    cout << dijkstra(n * m + m);
    return 0;
}